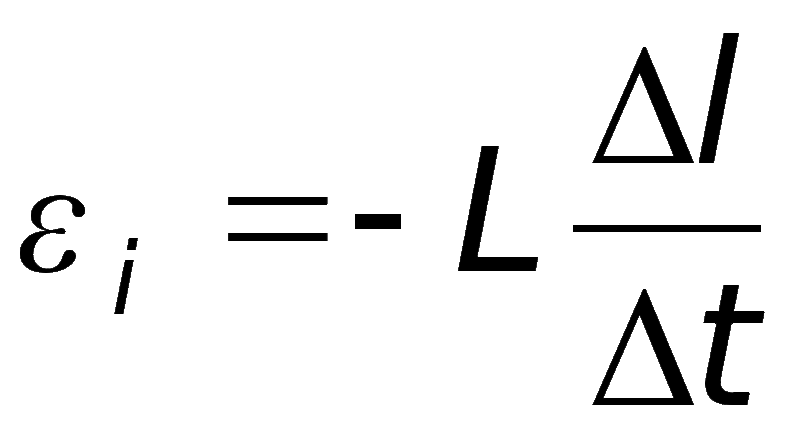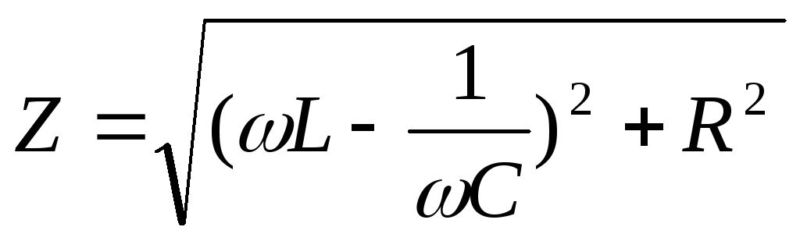Закон Ома для переменного тока катушки, участка цепи, типовых соединений — определение и формулы

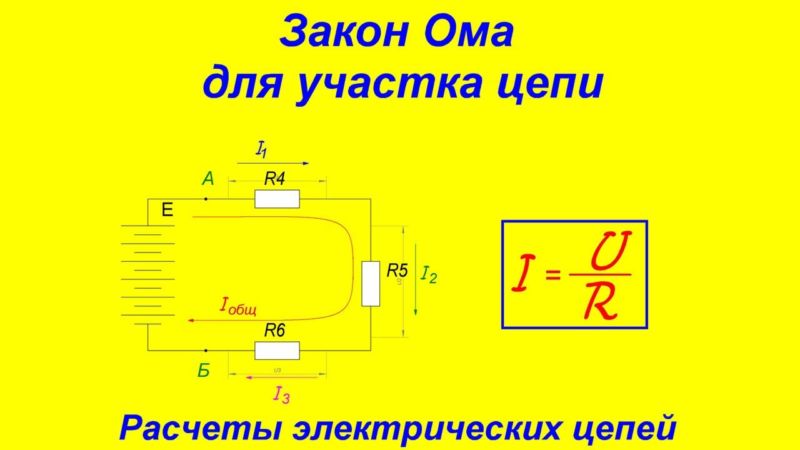
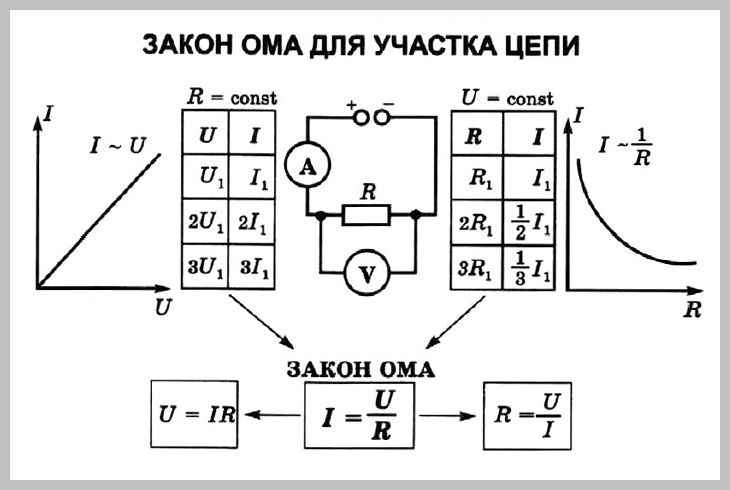
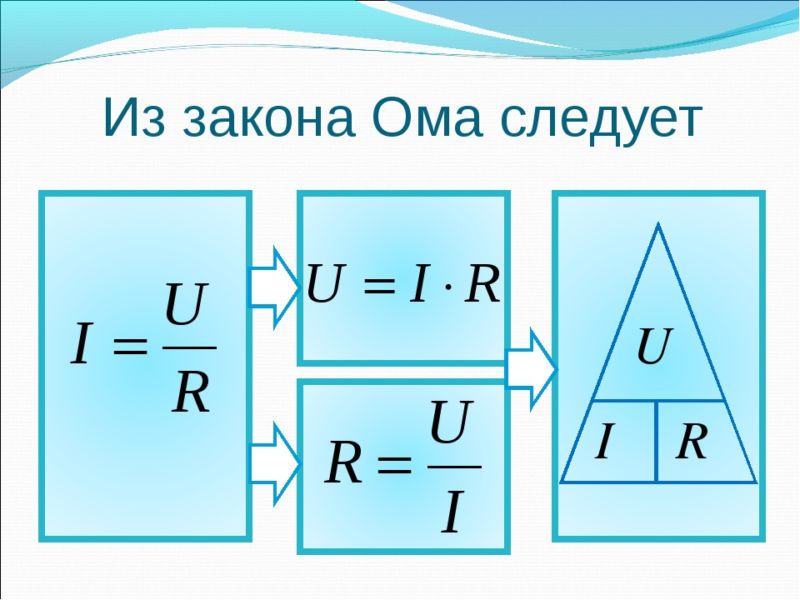
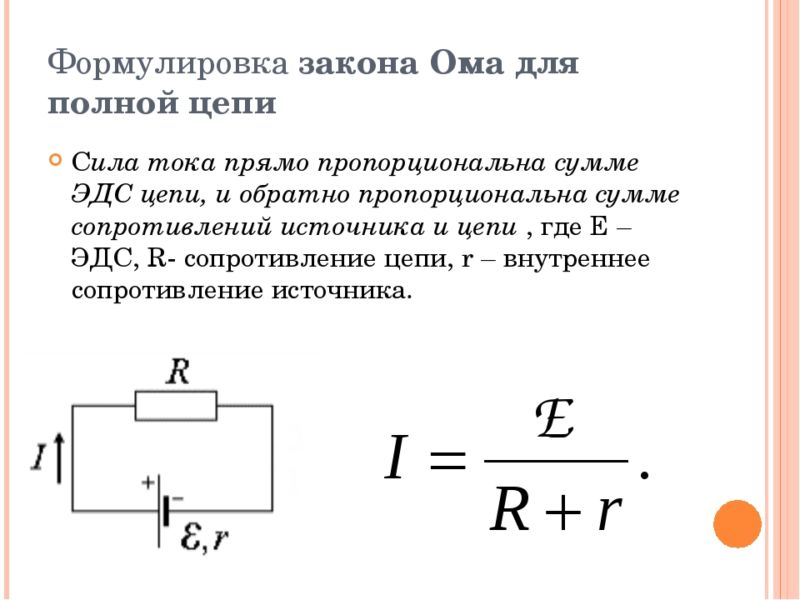
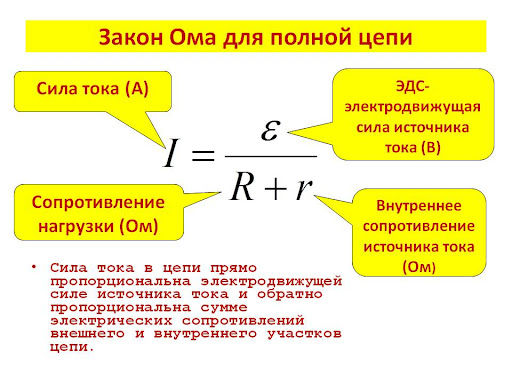
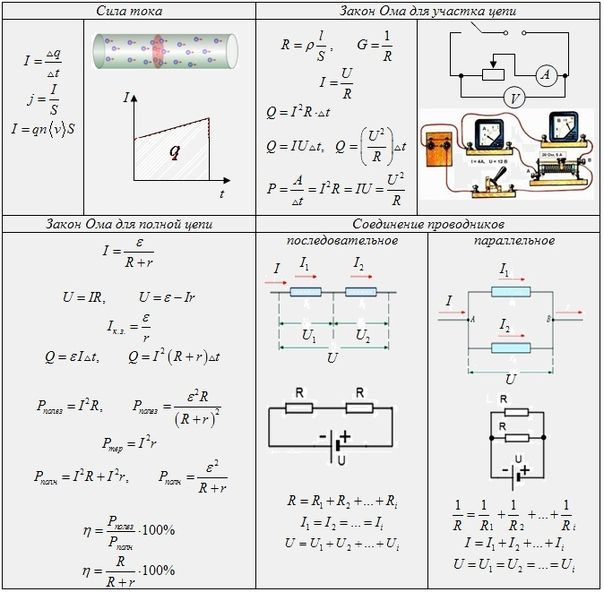
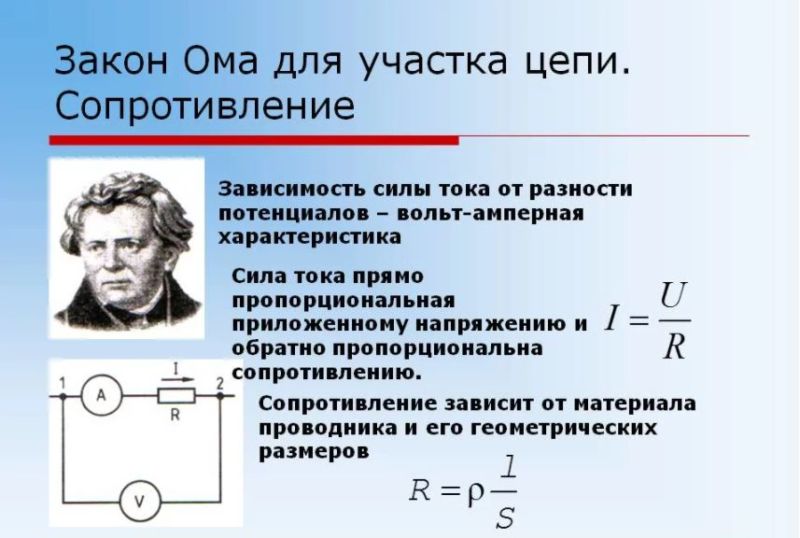
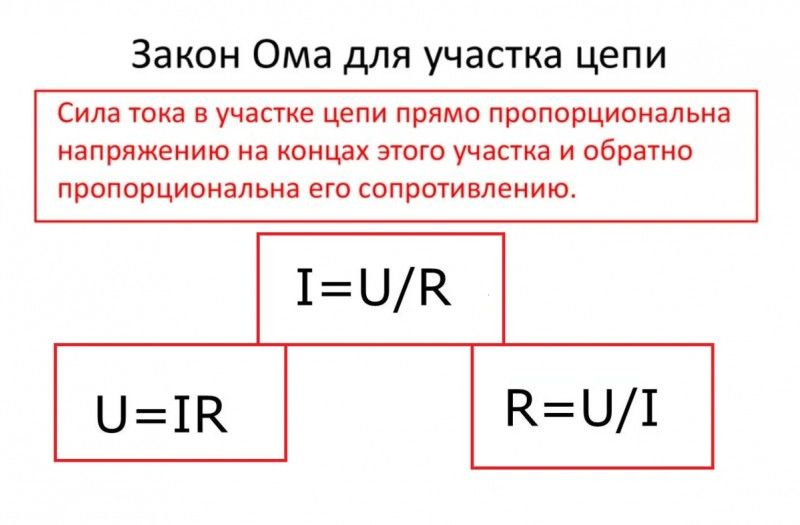
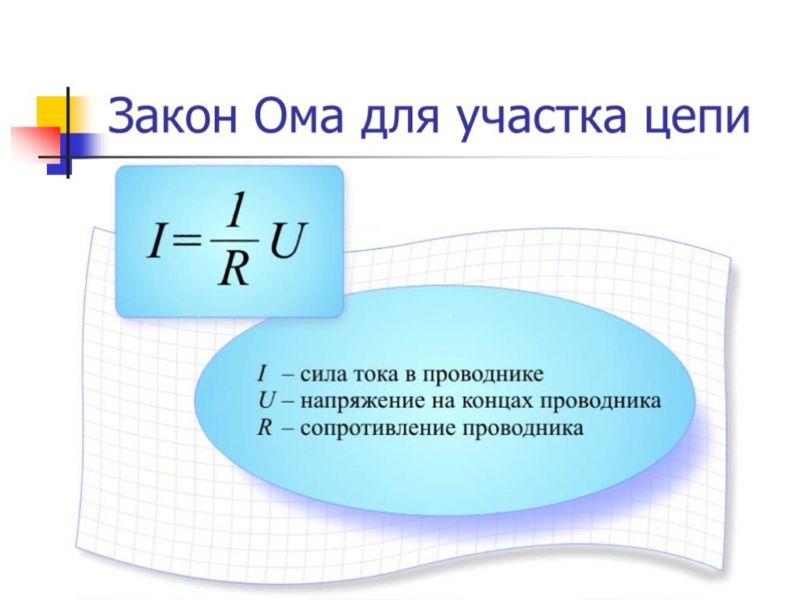
Для участка цепи, на котором отсутствует источник постоянной ЭДС, закон Ома связывает между собой три характеристики: силу тока (I), напряжение (U), сопротивление (R).

Математически закон записывают так: I = U/R.

Сила тока возрастает с увеличением на пряжения, уменьшением сопротивления.

В этой записи напряжение, сила тока не изменяются с течением времени. Для участков цепей с переменным током формула остается прежней, но следует учитывать, что величины U, I изменяются во времени с некоторой частотой. Для некоторых элементов она влияет на сопротивление.

Содержание

Особенности переменного напряжения, тока

Генераторы, вырабатывающие электроэнергию, сконструированы так, что напряжение, скорость изменения заряда в наших линиях электропередач меняются по гармоничному закону:

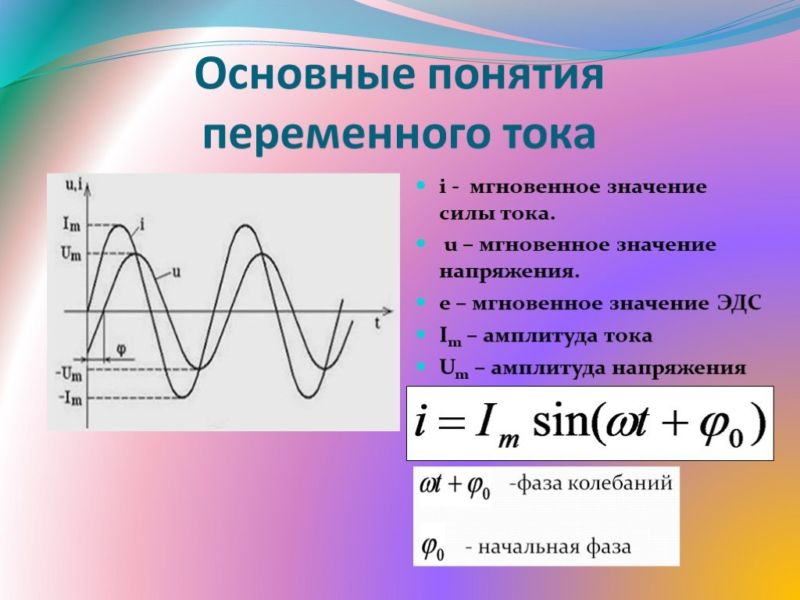
u = Umsin(ωt+φ0), i = Imsin(ωt+φ0).

Обозначения:

u, i – мгновенные значения (в произвольный момент времени);
Um, Im – амплитудные значения (максимальные);
Um – амплитуда напряжения;
Im – амплитуда тока;
t – время;
величина ω – циклическая частота.

Величина ω связана с линейной частотой ν выражением:

ω = 2πν:

π = 3,14 – математическая константа;
ν = 50 Гц (для электрических сетей в нашей стране).

Произведение ωt называют фазой:

ωt = φ.

Измеряют в радианах (рад), φ0 – начальная фаза, зачастую равна нулю. Использование в формулах функции cos не изменяет смысла физических выражений.

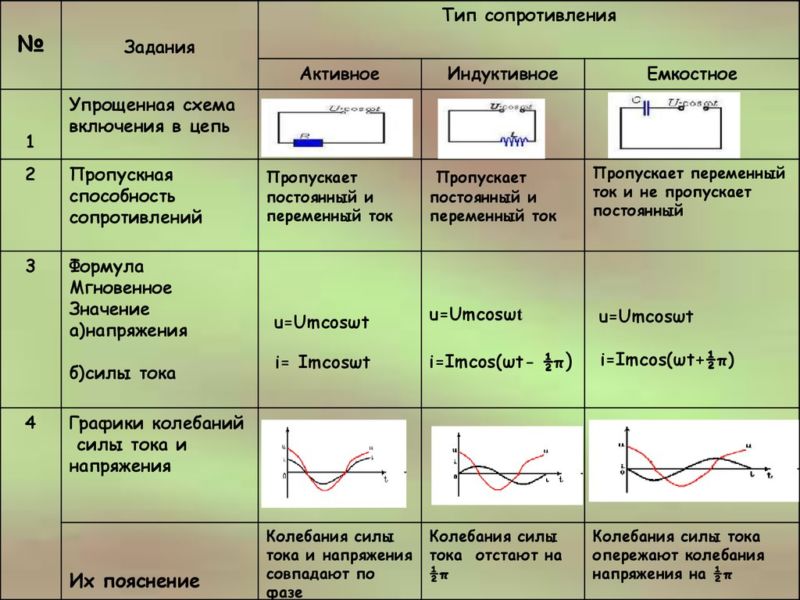
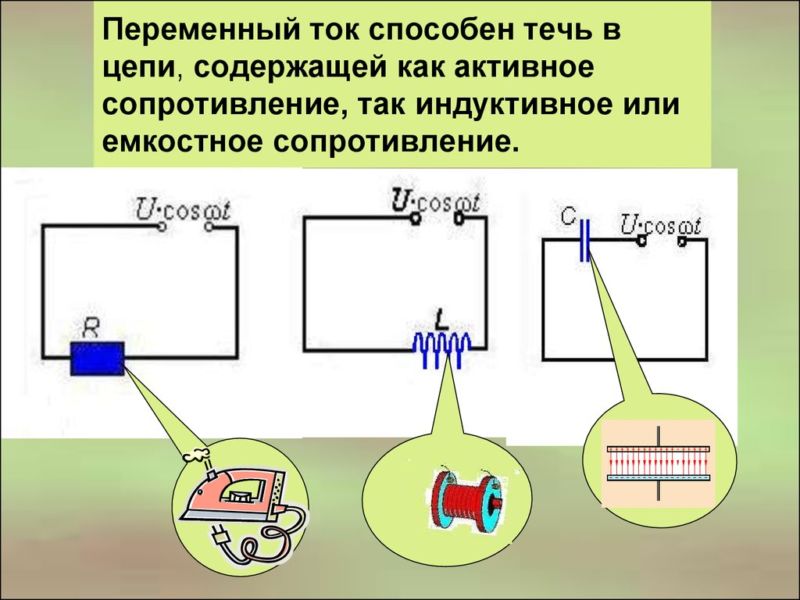
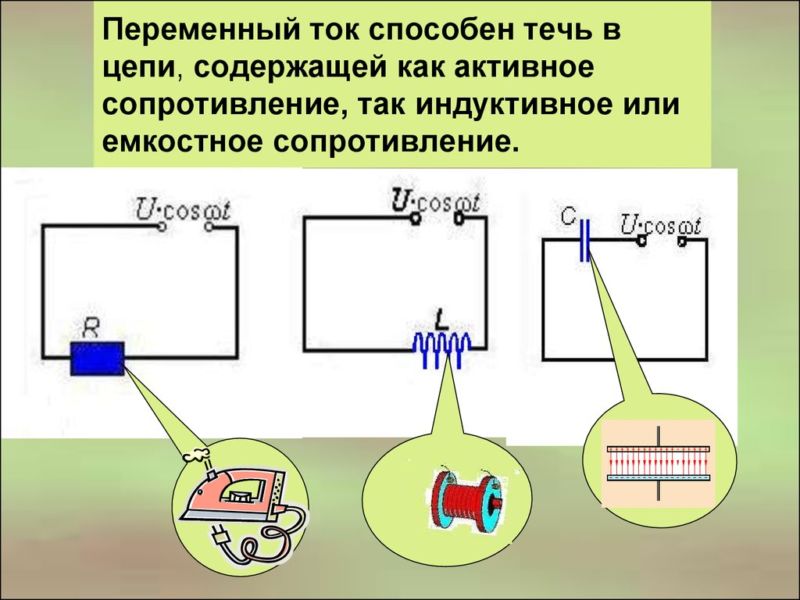
Если напряжение, изменяющееся по гармоничному закону, приложить к обычному резистору (в его роли может быть лампа накаливания, тепловой нагреватель), то через него начнут двигаться частицы, характер движения которых изменяется по такому же закону.

Изменение величин будет синхронным, фазы – одинаковыми. Такое сопротивление называют активным.

Эффективные значения

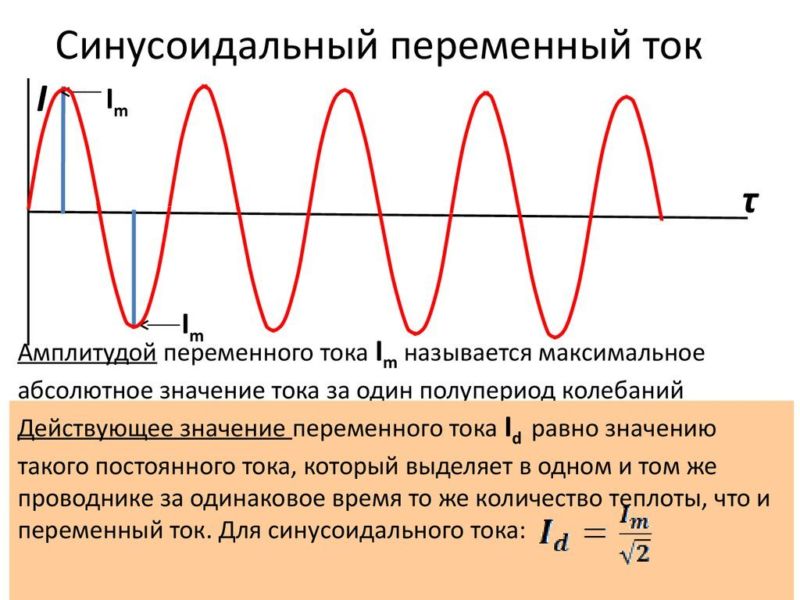
Среднее арифметическое значение напряжения, скорости изменения заряда за период равно нулю, поэтому его нельзя использовать для характеристики колебательного процесса. Квадраты этих величин, их средние значения всегда положительны.

Квадрат среднего значения силы тока равен половине квадрата амплитудного значения:

Is2 = Im2/2.

Is – среднее значение. Его называют еще эффективным (другое название – действующим):

Is = Im/√2.

Квадрат силы тока пропорционален количеству энергии, образующейся в проводнике: Q ~ Is2.

Эффективное значение величины переменного тока равно величине постоянного, при котором за время t = T образуется такое же количество теплоты. Для действующего значения напряжения формула аналогична:

Us = Um/√2.

Именно эффективные значения показывают измерительные приборы.

Происхождение индуктивного сопротивления

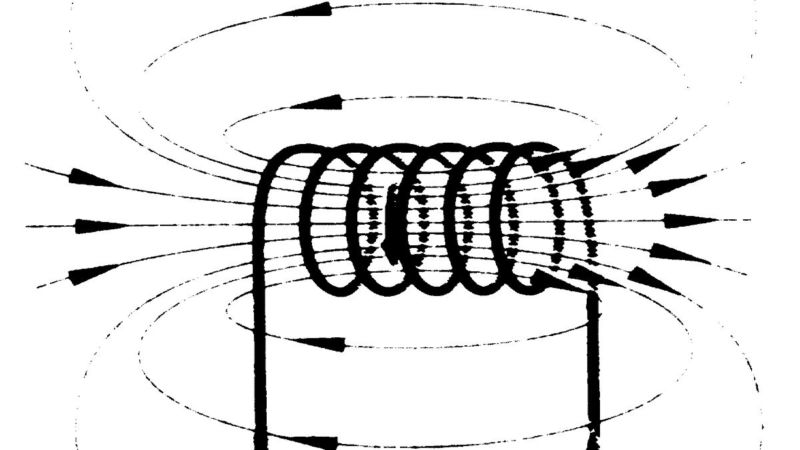
Вокруг проводника с движущимися заряженными существует магнитное поле. Оно слабое, но магнитная стрелка на него реагирует.

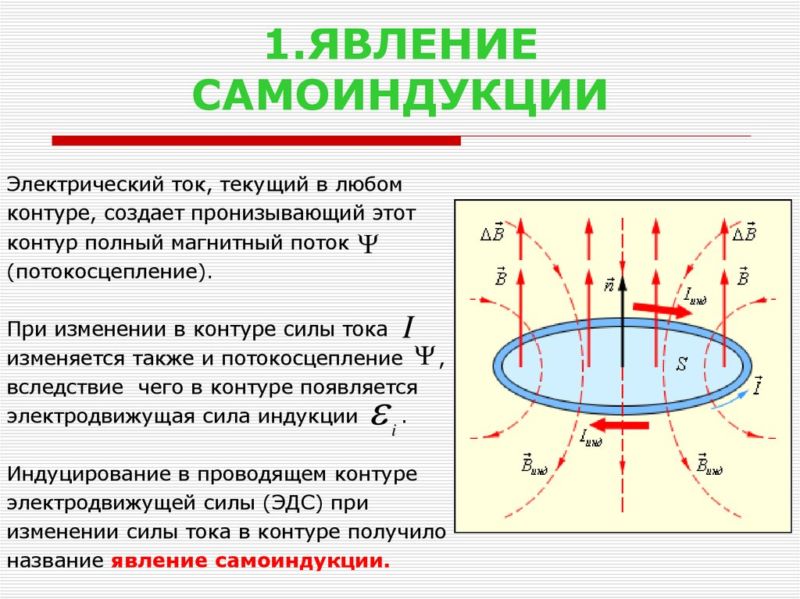
Если проводник намотать на катушку, то магнитное поле станет значительно более сильным. Оно приводит к появлению в катушке еще одного вида тока. Его возникновение в проводнике под действием магнитного поля называют электромагнитной индукцией. Обмотку называют катушкой индуктивности, а движение зарядов – индукционным током.

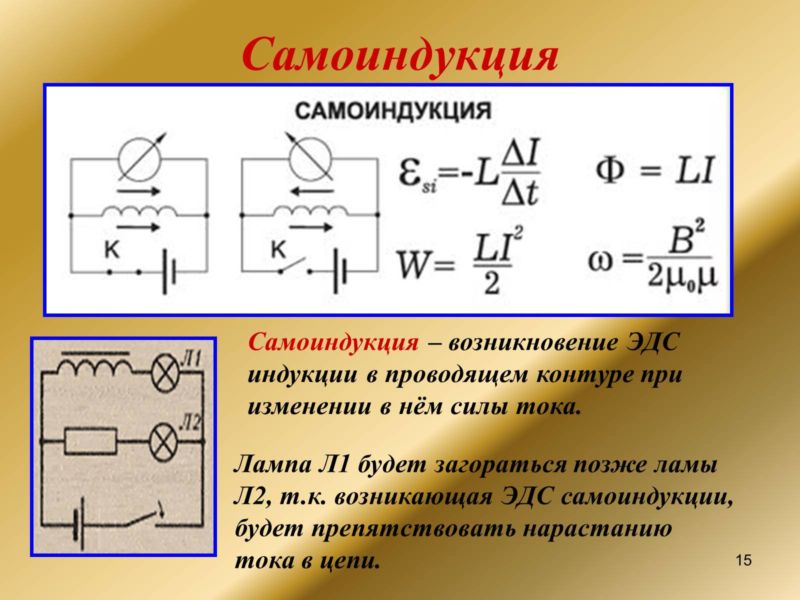
Одно из проявлений электромагнитной индукции – самоиндукция: возникновение дополнительной ЭДС в моменты резких изменений силы тока.

Это не колебания, возбуждаемые генератором, а изменения в момент включения, выключения, короткого замыкания. Для явления справедлива формула:

Esi = -L(ΔI/Δt).

Обозначения:

Esi – ЭДС самоиндукции;
ΔI – изменение силы тока;
Δt – промежуток времени;
L – индуктивность катушки, коэффициент самоиндукции.

Величина L – характеристика магнитных свойств катушки, измеряют ее в генри (Гн).

Индуктивность катушки равна 1 Гн, если при изменении в ней значения I на 1 А за 1 секунду возникает ЭДС самоиндукции 1 В.

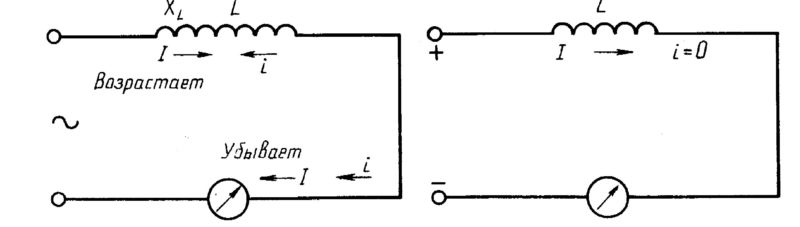
Закон Ома для катушки индуктивности

Индукционное магнитное поле тормозит движение по проводнику свободных зарядов. Это причина дополнительного (индукционного) сопротивления. Оно зависит от индуктивности L, частоты сигнала:

RL = ωL,

где RL – индуктивное сопротивление.

Зависимость характеристик для участка цепи с катушкой индуктивности приобретает вид:

I = U/RL.

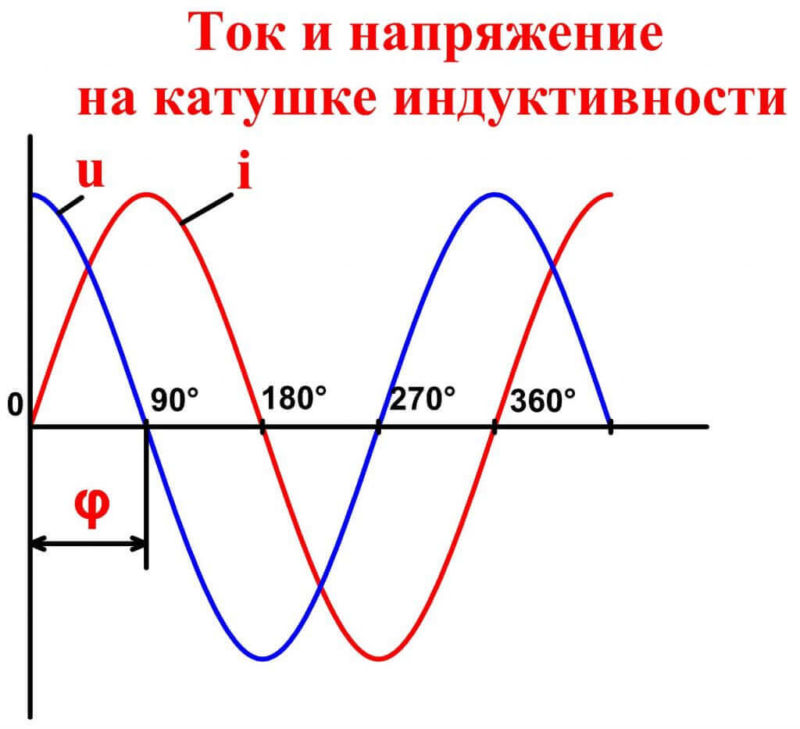
Катушка индуктивности имеет особенность: в ней колебания напряжения и скорости изменения заряда отличаются по фазе.

Колебания напряжения опережают колебания тока на четверть периода:

u = Umsinωt, i = Imsin(ωt – π/2).

Разность между значениями функции sin для 2 колебаний называют сдвигом фаз. Для индуктивной катушки:

ωt – (ωt – π/2) = π/2 = 90°.

Для наглядности сдвиг фаз Δφ изображают в виде векторной диаграммы. Участок цепи, в котором возникает разность фаз между колебаниями тока, напряжения называют реактивной нагрузкой.

Закон Ома для участка цепи с конденсатором

Для неизменного сигнала конденсатор представляет непреодолимое препятствие. Переменный сигнал проходит через него с некоторым усилием. Называют его емкостным сопротивлением.

Оно зависит от электроемкости конденсатора, частоты сигнала и обратно пропорционально произведению:

RC = 1/ωC.

Обозначения:

RC – емкостное сопротивление;
ω – круговая частота;
C – емкость конденсатора.

Зависимость величин для участка цепи с конденсатором записывают так:

I = U/RC.

Конденсатор – реактивная нагрузка. Колебания напряжения, скорости изменения заряда не синхронны. Изменение U отстает от колебаний I на четверть периода:

u = Umsinωt, i = Imsin(ωt + π/2).

Сдвиг фаз составляет 90°. Индуктивные, емкостные нагрузки сдвигают фазу в противоположных направлениях.

Закон Ома для типовых соединений

Резисторы, индуктивные катушки, конденсаторы соединяют несколькими способами:

все три элемента последовательно;
все три – параллельно;
два – параллельно, третий – последовательно с ними.

Запись закона Ома не изменяется, только есть отличие – в формуле для общего сопротивления.

Для цепей с активными, реактивными элементами оно называется полным или комплексным, его обозначают символом Z.

Поскольку на конденсаторе, катушке происходит сдвиг фаз, рассматривают не сами сопротивления, а их квадраты.

Катушка имеет активное сопротивление как проводник, индуктивное – как проявление электромагнитной индукции.

Цепь из резистора, катушки обозначают RL. В случае последовательного соединения полное сопротивление:

Z = √(R2 + RL2) = √(R2 + (ωL)2);

Зависимость I для этого случая:

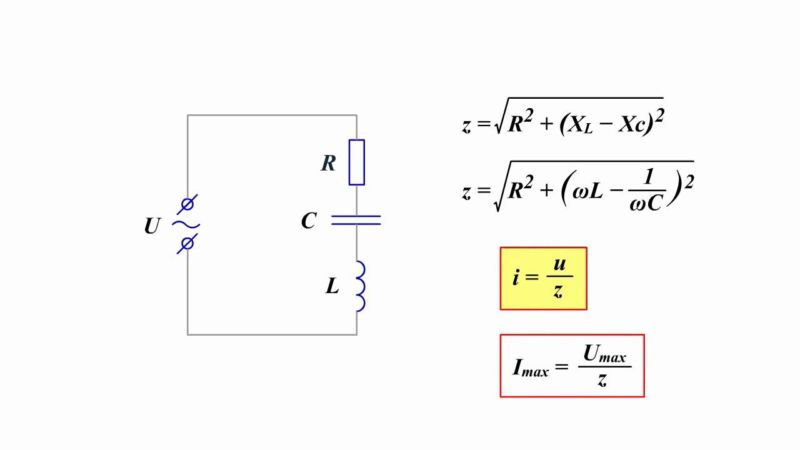
I = U/Z = U/√(R2 + ω2L2);

Участок с резистором и конденсатором – цепь RC. Для соединения последовательно:

Z = √(R2 + RC2) = √(R2 + (1/ωC)2);

Зависимость величин для этого соединения:

I = U/Z = U/√(R2 + (1/ωC)2)

Для соединения последовательно всех элементов (цепь RLC) значение полного сопротивления:

Z = √(R2 + (RL – RC)2) = √(R2 + (ω2L2 – (1/ω2C2)2)).

Комплексное сопротивление параллельного соединения находят из выражения:

1/Z2 = 1/R2 + 1/(RL2 – RC2).

Знание особенностей протекания переменного сигнала в цепи с конденсатором, индуктивной катушкой помогает в расчете радиотехнических цепей. Реактивные элементы используют в фильтрах верхних, нижних частот. Явление возникновения колебаний, резонанса широко применяют в современных средствах связи.